백준 1697번 숨바꼭질 (Java)

해결과정

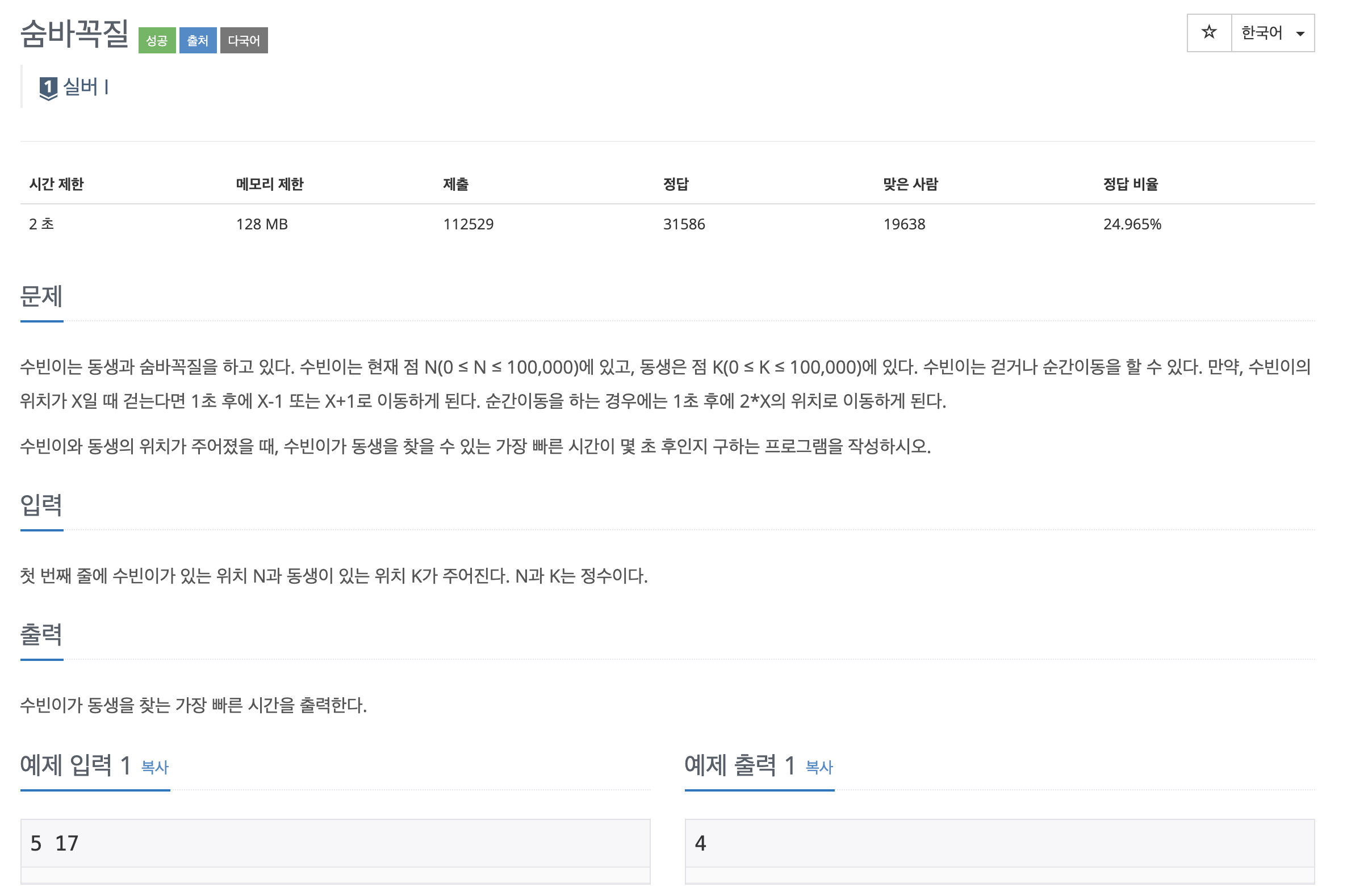
전형적인 브루트 포스 형태의 문제이다.

문제는 수빈이와 동생의 위치가 일치되는 지점을 찾고 거기까지 걸리는 최소 시간을 찾는 문제이다.

재밌는 것은 위치는 선형적으로 계산하면 되고, 순간이동이라는 선택지가 있다는 것이다.

따라서, 각 이동시점마다 선택할 수 있는 선택지는 3개이다. 이러한 선택지와 과정들을 탐색하면서 가장 빠른 시간에 일치되는 시점을 찾는 것이다.

 

처음에는 DFS로 접근을 했는데, 이렇게 됐을 경우 StackOverFlow가 발생했다.

왜냐하면, 재귀적으로 호출하기 때문에 운이 좋으면 바로 찾아낼 수 있지만, 잘못된 과정으로 진입한다면 100000이 넘어서는 지점까지 계속해서 재귀호출을 하기 때문이다. 예를 들어, X+1 호출이 맨 처음 선택지로 주어진다면 재귀 호출은 100000이 될 때까지 X+1 이동을 호출할 것이다. 함수는 100000번 호출하게 되고 그만큼 스택 프레임에 부하가 발생할 수 밖에 없다.

 

따라서, BFS로 접근을 수정했다. 각 노드마다 3개의 가지치기를 하며, boolean 배열을 통해 중복 방문을 방지했다. while 문 안에서는 노드를 꺼낼 때마다 동생의 위치와 일치하는지 판단하는 조건문을 통해 while 루프 종료 시점을 지정했다.

 

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

public class Main {
    static int min = 0;
    static boolean[] visited = new boolean[100001];

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        int n = scanner.nextInt();
        int k = scanner.nextInt();

        moveBfs(n, k);

        System.out.println(min);
    }

    static void moveBfs(int x, int k) {
        Queue<int[]> queue = new LinkedList<>();
        queue.add(new int[]{x, 0});

        while (!queue.isEmpty()) {
            int[] point = queue.poll();
            int curX = point[0];

            if (curX == k) {
                min = point[1];
                return;
            }

            visited[curX] = true;

            if (check(curX+1)) {
                queue.add(new int[]{curX+1, point[1]+1});
            }
            if (check(curX-1)) {
                queue.add(new int[]{curX-1, point[1]+1});
            }
            if (check(curX*2)) {
                queue.add(new int[]{curX*2, point[1]+1});
            }
        }
    }

    static boolean check(int x) {
        if (x < 0 || x > 100000 || visited[x]) {
            return false;
        }

        return true;
    }
}